- 综合知识导航
- 数据仓库略谈
- 智能制造定义及实现智能制造的意义
- 开源分布式数据库Hbase
- 数据库与大数据数据仓库区别
- MATLAB数据可视化
- 数据仓库简史及特点
- 浅谈如何在前端实现数据可视化热力图
- 18个数据可视化在生活中的应用
- 一文看懂:24种图表数据可视化的优缺点对比
- 10个数据可视化例子,让你更懂可视化
- 经典面试题:说说ETL的过程
- 15个惊艳业界的数据可视化作业案例
- 18篇最好看的数据可视化作品赏析
- 来了解一下数据可视化平台FineBl
- 数据可视化的过程有哪四个
- excel数据可视化图表制作
- 信息可视化设计用什么软件?一个工具,帮你实现酷炫的数据可视化
- FineBI——免费的数据可视化工具软件
- 帆软:做好企业发展的“导航”!
- 大数据数据仓库—概念
- 12个惊艳的数据可视化优秀案例
- 有趣好看的数据可视化图表怎么制作?
- R语言数据可视化分析怎么做
- 数据仓库管理系统与全链路数据体系
- 详解数据数据仓库有哪五层架构
- 数据统计可视化报表设计形式
- 商业智能软件市场 帆软何以独占鳌头?
- 大数据时代下的大数据舆情监测与分析
- 八大数据分析模型一览
- 数据可视化的工具有哪些
- 简述面向航空公司IT的“QAR数据分析系统”
- 数据仓库建模的三种模式
- 数据可视化图表怎么做才对
- 数据仓库的ETL、OLAP和BI应用
- 仓库管理系统选择指南
- 数据可视化需要了解什么
- 优秀的数据可视化怎么做的
- 五个数据分析可视化案例讲解
- 大数据可视化分析有哪四个步骤
- 如何利用插件制作Excel数据可视化图表
- 详解数据仓库搭建步骤
- 基于Hadoop的数据分析平台搭建
- 话说数据仓库分层4层模型
- Excel也有很强大的数据分析工具!
- 数据仓库概念及概述
- 数据挖掘实际案例——想上大学的有哪些人
- 优质数据分析报告的13个要点
- 来说数据仓库建模
- Python数据分析是干嘛的,需要哪些步骤?
- 闲说数据仓库理论上的范式
- 一文罗列数据集市和数据仓库的区别
- 数据分析之数据加工
- ELT数仓技术
- hive和hbase的区别有哪些
- 搭建hive运行环境详解
- 略讲数仓
- 大数据分析中,有哪些常用的大数据分析模型?
- 大数据分析中,有哪些常用的大数据分析模型?
- 数据分析技能
- 如何用R Markdown生成R语言数据分析报告
- 一文读懂基于大数据的数据仓库建设!
- 数据仓库发展趋势(1996-)
- 数据仓库的来源和发展
- 细讲ods数据仓库
- druid kylin 对比
- 数据仓库怎么建立需求?
- 听说过数据库,那数据仓库是做什么的
- 细说数据仓库与数据库的区别
- 开源数据仓库解决方案GreenPlum
- 如何构建数据仓库,本文细讲
- ETL处理流程与技术架构
- 数据治理ETL解决方案
- 数据仓库的多维数据模型设计
- olap与数据仓库的关系及区别
- SQL etl的数据指纹
- 数据仓库 数据湖的区别
- ETL是做什么?学习后有什么用?本文这就告诉你!
- 数据中台 数据仓库的区别
- 数据仓库的分层,你知道吗?
- 谈谈数仓etl系统建设
MATLAB数据可视化
数据可视化
数据可视化(Data Visualization)是指运用计算机图形学和图像处理技术,将数据转换为图形或图像在屏幕上显示出来,并进行交互处理的理论、方法和技术。它涉及计算机图形学、图像处理、计算机辅助设计、计算机视觉及人机交互技术等多个领域。该技术的主要特点如下。
(1)交互性:用户可以方便地以交互的方式管理和开发数据。
(2)多维性:可以看到表示对象或事件的数据的多个属性或变量,而数据可以按其每一维的值,将其分类、排序、组合和显示。
(3)可视化:数据可以用图像、曲线、二维图形、三维图形和动画等来显示,并可对其模式和相互关系进行可视化分析。
数据可视化可以大大加快数据的处理速度,令时刻都在产生的大量数据得到有效的利用;可以在人与数据、人与人之间实现图像通信,从而使人们能够观察到数据中隐含的线索,为发现和理解科学规律提供了力的工具;可以实现对计算和编程过程的引导和控制,通过交互手段改变过程所依据的条件,并观察其影响。
数据可视化有助于工程过程的一体化和流线化,并能使工程的领导和技术人员看到和了解过程中参数的变化对整体的动态影响,从而达到缩短研制周期、节省工程全寿命费用的目的。
在前面已经介绍和分析了MATLAB数据可视化处理、运算和分析中的各种应用。和其他类似的科学计算工具相比,MATLAB数据可视化图形编辑功能显得尤为强大。通过图形,用户可以直观地观察数据间的内在关系,也可以十分方便地分析各种数据结果。从最初的版本开始,MATLAB就一直致力于数据的图形表示,而且在更新版本的时候不断地使用新技术来改进和完善可视化的功能。MATLAB R2014b 推出了全新的 MATLAB 图形系统。全新的默认颜色、字体和样式便于数据解释。抗锯齿字体和线条使文字和图形看起来更平滑。图形对象便于使用–您可以在命令窗口中显示常用属性,并且对象支持熟悉的结构化语法,可以更改属性值。
本章介绍MATLAB数据可视化中的绘图方法,以及如何编辑图形、标记图形等。
7.1 绘图的基本知识
7.1.1 离散数据和离散函数的可视化
众所周知,任何二元实数标量对可以用平面上的一个点表示,任何二元实数“向量对”可以用平面上的一组点表示。对于离散实函数,当以递增(或者递减)的次序取值时,根据函数关系可以求得同样数目的。当把所对应的向量用直角坐标中的点序列图示时,就实现了离散函数的可视化,当然图形上的离散序列所反映的只是某些确定的有效区间内的函数关系。需要注意的是:图形不能表现无限区间上的函数关系,这是由图形的原理决定的,并不是MATLAB软件本身的限制。
【例7-1】 用图形表示离散函数。
![]()
Ex_7_1.m
n=0:12;
y=1./abs(n-6); % 准备离散点数据
plot(n,y,’r*’,’MarkerSize’,20) % 绘图
grid on
以上代码运行的结果如下,得到的图形如图7-1所示。
7.1.2 连续函数的可视化
与离散函数可视化一样,进行连续函数可视化也必须先在一组离散自变量上计算相应的函数值,并把这一组“数据对”用点图示。但这些离散的点不能表现函数的连续性。为了进一步表示离散点之间的函数情况,有两种常用的处理方法:(1)对区间进行更细的分割,计算更多的点,去近似表现函数的连续变化;(2)把两点用直线连接,近似表现两点间的函数形状。
在MATLAB中,以上两种方法都可以采用。但需注意:倘若自变量的采样点数不够多,则无论使用哪种方法都不能真实地反映原函数。
【例7-2】 用图形表示连续调制波形。
![]()
Ex_7_2.m
t1=(0:11)/11*pi; % 自变量
y1=sin(t1).*sin(9*t1); % 对应的函数值
t2=(0:100)/100*pi;
y2=sin(t2).*sin(9*t2);
% 以下为绘图,将几个图作为子图放在一起便于比较
subplot(2,2,1),plot(t1,y1,’r.’),axis([0,pi,-1,1]),title(‘子图 (1)’)
subplot(2,2,2),plot(t2,y2,’r.’),axis([0,pi,-1,1]),title(‘子图 (2)’)
subplot(2,2,3),plot(t1,y1,t1,y1,’r.’)
axis([0,pi,-1,1]),title(‘子图 (3)’)
subplot(2,2,4),plot(t2,y2)
axis([0,pi,-1,1]),title(‘子图 (4)’)
以上代码运行的结果如图7-2所示。
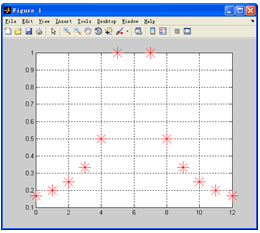
图7-1 离散函数的可视化
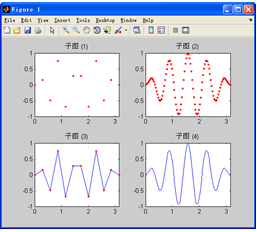
图7-2 连续函数的可视化
7.1.3 可视化的一般步骤
本小节介绍可视化的一般步骤,其目的是让读者对图形的绘制过程有一个宏观的了解,如表7-1所示。具体细节将在后面介绍。
表7-1 绘制图形的一般步骤
| 步 骤 | 典型命令 |
| 1.数据准备
选定所要绘图的范围 产生自变量采样向量 计算相应的函数值向量 |
t=pi*(0:100)/100
y=sin(t).*sin(9*t); |
| 2.选定图形窗口及子图位置
默认打开Figure. 1,或当前窗口,或当前子图。可以用命令指定图形窗口和子图位置 |
figure(1)
subplot(2,2,3) |
| 3.调用绘图命令(可以包括线型、色彩、数据点型) | plot(t,y,‘b-’) % 用蓝色实线绘图 |
| 4.设置轴的范围与刻度、坐标网格 | axis([0,pi,-1,1]) % 设置轴的范围
grid on % 画坐标网格 |
| 5.图形注释:
图名、坐标名、图例、文字说明等 |
title(‘figure’) % 图名
xlabel(‘t’); ylabel(‘y’) % 轴名 legend(‘sin(t)’, ‘sin(t)。*sin(9*t)’) % 图例 text(2,0.5,‘y=sin(t).*sin(9*t)’)% 文字说明 |
| 6.图形的精细修饰
利用对象属性值设置,利用图形窗口工具栏设置 |
set(h,‘MarkerSize’,10)
% 设置数据点大小 |
| 7.图形的导出与打印 | % 采用图形窗口菜单操作 |
步骤1和3是最基本的绘图步骤。一般来说,用这两个步骤所画的图形已经具备足够的表现力,其他步骤并不是必须的,另外其他步骤的输入顺序也可以根据用户的需要或者喜好随意指定,一般情况下并不影响输出结果。二维绘图和三维绘图的基本步骤差不多,只是三维绘图多了一些属性控制操作方面的选择。


评论区(0)