非线性回归

1、可线性化的非线性分析

变量之间的非线性形式较多，较为常见的形式如下图：

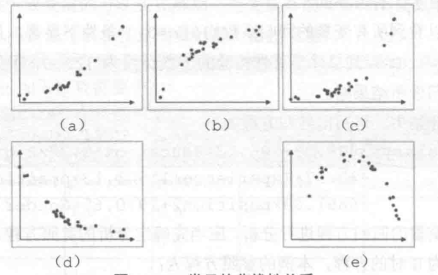
非线性形式的变量关系一般可以通过变量代换或转换的方式转化为线性关系。横纵轴所代表变量之间的关系为幂函数形式的关系，即可建立的模型为：

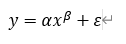
其中a、β为模型参数，ε为误差项。

在实际建模过程中，可以把上述模型左右变量同时取对数，可得：

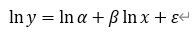
令y’=lny，x’=Inx，a’=Ina 可得如下模型：

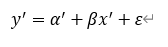
类似的，对数模型y=a+βInx+ε，可以转换成y=a+βx’+ε的线性形式；

指数模型：

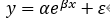
对上式两边同时取对数，可得Iny=lna+βx+ε，再用变量代换转换为y’=a’+βx+ε的线性形式；

逻辑斯蒂(Logistic)模型：

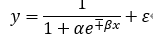
可以转换为：

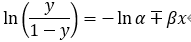
再使用变量代换的形式转换成线性形式；

抛物线模型同理也可作类似处理。

类似的，在存在多个自变量情形下的非线性回归，也可以按照上述变量转换和代换的方式把多元非线性模型转化为多元线性模型。

2、非线性回归模型

对常见非线性模型进行线性转换后用线性回归的参数估计方法进行参数估计虽然较简单，但有时估计效果不理想。当对因变量y作变换时，由于线性回归的最小二乘估计是对变换后的y而不是直接对y进行估计，在此基础上估计的曲线可能会造成拟合效果并不理想。此外，有些时候变量间的曲线关系比较明显，关系式也已知，但是难以用变量变换或代换的方式将其线性化，这个时候可以考虑直接使用非线性最小二乘估计方法来估计模型参数。

此外，非线性回归模型还有一种情况:模型中至少有一个参数不是线性的，该模型也可称之为非线性模型。如有如下模型：

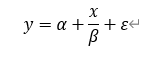
对模型右边求偏导数并利用回归模型经典假定，得到：

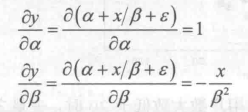
由上述第二个偏导数得知，自变量对因变量的影响还会受到参数β本身的影响，而自变量β通过对因变量发生的作用并不是线性的。这种模型可称之为非线性回归模型。

非线性模型的参数一般可以使用最小二乘及迭代算法进行估计，主要估计方法有最速下降法(Steepest-Descent)或梯度法(Gradient Method)、牛顿法( Newton Method)、修正高斯-牛顿法(Modified Gauss-Newton Method)和麦夸特法(Marquardt Method)等。一般而言，非线性曲线的拟合程度均较高，在考虑实际数据的拟合问题时，一般的分析过程往往不会给出模型检验结果。

一元线性回归多项式回归

评论区（0）

非线性回归

1、可线性化的非线性分析

2、非线性回归模型

评论 取消

评论取消