回归分析的基本原理

回归分析的基本原理

回归分析与相关分析在理论和方法上具有一致性，变量之间没有关系，就谈不上回归分析或建立回归方程：相关程度越高，回归效果就越好，而且相关系数和回归系数方向一致，可以互相推算。

相关分析中的两个变量之间的地位是对等的，即变量A与变量B相关等价于变量B与变量A相关，相关分析的两个变量均为随机变量;而回归分析中要确定自变量和因变量，通常情况下只有因变量是随机变量，人们可以利用回归分析来对研究对象进行预测或控制。

回归分析往往是通过一条拟合的曲线来表示模型的建立。以线性回归为例，设y表示因变量，x表示自变量，则有如下线性回归模型：

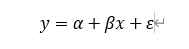
其中：a和β是回归模型的参数，称为回归系数(a也可称为截距项)； ε是随机误差项或随机扰动项，反映了除x和y之间线性关系之外的随机因素或不可观测的因素。

通常在回归分析中，对ε有如下最为常用的基本经典假定：

1. ε的期望值为0
2. ε对于所有x而言具有同方差性
3. ε是服从正态分布且相互独立的随机变量

如果存在多个自变量，回归模型可以写作：

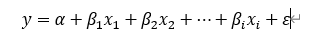
因为上述直线模型中含有随机误差项，所以回归模型反映的直线是不确定的。回归分析的主要目的就是要从这些不确定的直线中，找出一条最能够代表数据原始信息的直线，来描述因变量和自变量之间的关系，这条直线称之为回归方程，如只有一个自变量的情况下，可对模型左右两边取x的条件期望并根据ε的经典假定，可得：

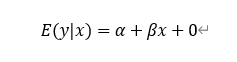
然后通过一定的参数估计方法，可得到估计的直线方程如下：

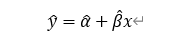
1、最小二乘法

Python实现：

# -*- coding: utf-8 -*-
import numpy as np  #惯例
import scipy as sp  #惯例
from scipy.optimize import leastsq #这里就是我们要使用的最小二乘的函数
import pylab as pl 

m = 9  #多项式的次数

def real_func(x):
    return np.sin(2*np.pi*x) #sin(2 pi x) 

def fake_func(p, x):
    f = np.poly1d(p) #多项式分布的函数
    return f(x)

#残差函数
def residuals(p, y, x):
    return y - fake_func(p, x) 

#随机选了9个点，作为x
x = np.linspace(0, 1, 9)

#画图的时候需要的“连续”的很多个点
x_show = np.linspace(0, 1, 1000) 
y0 = real_func(x)

#加入正态分布噪音后的y
y1 = [np.random.normal(0, 0.1) + y for y in y0] 

#先随机产生一组多项式分布的参数
p0 = np.random.randn(m) 

plsq = leastsq(residuals, p0, args=(y1, x))
print('Fitting Parameters ：', plsq[0]) #输出拟合参数
pl.plot(x_show, real_func(x_show), label='real')
pl.plot(x_show, fake_func(plsq[0], x_show), label='fitted curve')
pl.plot(x, y1, 'bo', label='with noise')
pl.legend()
pl.show()

输出的拟合参数为：

输出的图像为：

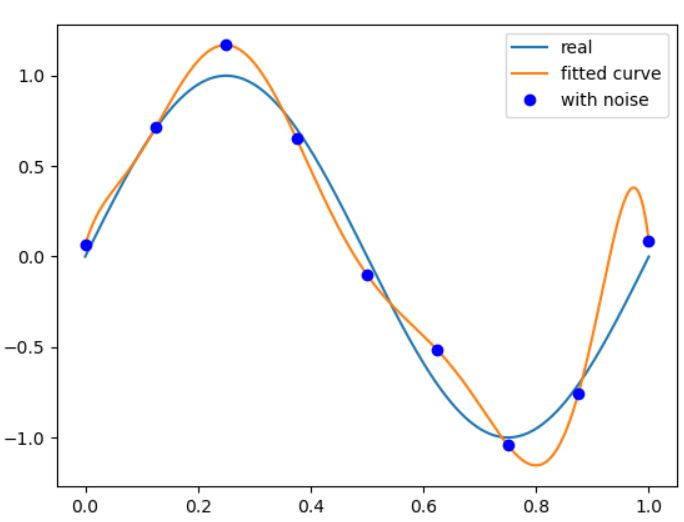
可把具体某个因变量的观测值、期望值、估计值做如下定义：

那么如何在存在随机因素的回归模型中找出最能代表原始数据信息的回归直线呢？可以通过对因变量的离差入手进行分析。

这种参数估计的方法和过程是在随机误差项ε是一个期望值为0，且对于所有x而言具有同方差性，服从正态分布且相互独立的假定下进行的，通常被称之为“普通最小二乘法” (OLS, ordinary least squares)。 由上述通过条件期望形式使用普通最小二乘估计出来的参数估计值，代表了自变量变动对因变量期望变量的影响。