面试 (MySQL 索引为啥要选择 B+ 树)

前言:

每天都在跟 mysql 打交道，你知道执行一条简单的 select 语句，都经历了哪些过程吗？

首先，mysql 主要是由 server 层和存储层两部分构成的。server 层主要包括连接器、查询缓存，分析器、优化器、执行器。存储层主要是用来存储和查询数据的，常用的存储引擎有 InnoDB、MyISAM，MySQL 5.5.5 版本后使用 InnoDB 作为默认存储引擎。

连接器
连接器主要负责将 mysql 客户端和服务端建立连接，连接成功后，会获取当前连接用户的权限。这里获取到的权限对整个连接都有效，一旦连接成功后，如果使用管理员账号对该用户更改权限，当前连接中的拥有的权限保持不变，只有等到下次重新连接才会更新权限。

查询缓存
连接成功后，即开始要正式执行 select 语句了，但是在执行查询之前，mysql 会去看下有没有该条语句的缓存内容，如果有缓存直接从缓存中读取并返回数据，不再执行后面的步骤了，结束查询操作。
如果没有缓存则继续往后执行，并将执行结果和语句保存在缓存中。
注意在 mysql8 后已经没有查询缓存这个功能了，因为这个缓存非常容易被清空掉，命中率比较低。只要对表有一个更新，这个表上的所有缓存就会被清空，因此你刚缓存下来的内容，还没来得及用就被另一个更新给清空了。
分析器
既然没有查到缓存，就需要开始执行 sql 语句了，在执行之前肯定需要先对 sql 语句进行解析。分析器主要对 sql 语句进行语法和语义分析，检查单词是否拼写错误，还有检查要查询的表或字段是否存在。
如果分析器检测出有错误就会返回类似 “You have an error in your sql” 这样的错误信息，并结束查询操作。
优化器
通过分析器之后，mysql 就算是理解了你要执行的操作了。通常对于同一个 sql 语句，mysql 内部可能存在多种执行方案，比如存在多个索引时，该选择哪个索引，多个表关联查询时，怎么确认各个表的连接顺序。
这些方案的执行结果都一样，但是执行效率不一样，所以 mysql 在执行之前需要尝试找出一个最优的方案来，这就是优化器的主要工作。但是 mysql 也会有选择错误方案的时候，这里暂不细说，留到后面再解释原因。
执行器
经过优化器选定了一个方案后，执行器就按照选定的方案执行 sql 语句。前面我们有讲过，在连接器中会读取当前用户的权限，连接器中只是获取权限而已，并没有对权限进行判断和校验。
所以在执行器中，在执行语句之前会判断权限，如果没有对应的权限则会直接返回并提示没有相关权限。
这里你可能会问，为什么不在连接器中就直接判断权限呢，这里我觉得可能是因为 mysql 要查询的表并不一定仅限于 sql 语句中字面上的那些表，有的时候可能需要经过分析器和优化器之后才能确定到底要怎么执行，所以权限校验放在执行器中是有道理的。
注意如果是在前面的查询缓存中查到缓存之后，也会在返回结果前做权限校验的。
权限校验通过之后，就继续打开表，调用存储引擎提供的接口去查询并返回结果集数据。
到这里，一条查询 sql 语句就执行结束了。

开始
不知道你有没有这种感觉，那些所谓的数据结构和算法，在日常开发工作中很少用到或者几乎不曾用到，可能只是在每次换工作准备面试的时候才会捡起来学习学习。

那我希望今天这篇文章能让你对数据结构的具体应用能有个初步的概念，就像上面说的一样，先从我们每天都在用的 mysql 数据库说起吧。

首先，mysql 主要是由 server 层和存储层两部分构成的。server 层主要包括连接器、查询缓存，分析器、优化器、执行器。存储层主要是用来存储和查询数据的，常用的存储引擎有 InnoDB、MyISAM，MySQL 5.5.5 版本后使用 InnoDB 作为默认存储引擎。

我们主要讨论 mysql 的存储层，不同的存储引擎其底层的数据结构是不一样的，我们这里就以默认的 InnoDB 为例，所以严格来说应该是 InnoDB 为啥要选择 B+ 树这种数据结构来存储数据。

在文章正式开始之前，你先要知道 mysql 中的 InnoDB 在底层是采用 B+ 树这种数据结构来存储数据的。你先记住就好了，下面我们再来一步一步解释为什么。

几种常见的数据结构

首先你要知道，mysql 的索引主要是为了提高查询效率的，那一定得找一个合适的数据结构来存储数据，哈希表、数组、二叉搜索树这三种常见的数据结构都可以提高查询效率。

哈希表
哈希表就是一种以键值对来存储数据的结构，你可以通过一个 key 就可以很快的查询出对用的 value 值。哈希表主要是利用了数组的随机访问特性，实现思想主要是通过一个哈希函数把 key 转换成一个哈希值，这个哈希值就对应数组中的某个下标。
但是由于哈希表是无序的，区间查询效率会非常的慢，所以哈希表通常只用于查询单个值。
有序数组
数组就好说了，数组具有连续性和随机访问特性，因此数组都能很高效的进行单个等值查询和区间查询，但是 mysql 不仅仅是查询数据，还会有插入和删除数据的操作。
在有序数组中插入或删除一个数据会需要批量移动数组中其他数据，这是一个不小的消耗，影响性能。因此有序数组适合处理静态数据，比如一些过往的不会再修改的数据。
在这里你可能会问，既然哈希表其实也是利用了数组的特性，那有了数组为啥还需要哈希表呢。是因为数组下标 key 只能是数字，而哈希表可以支持字符串 key，哈希函数可以把这个 key 转换成一个数组下标。
同时，不同的 key 如果通过哈希函数转换成了相同的数组下标，这就会造成冲突，在哈希表中一般会通过再拉出一个链表来保存这个冲突的值。
二叉搜索树
注意，二叉搜索树和二叉树不一样，二叉树是指每个节点的左儿子小于父节点，父节点又小于右儿子，即二叉搜索树的中序遍历就是一个有序序列。
由于索引不仅仅是存在内存中，还会存储在硬盘中，因此就会涉及到 IO 性能了，就要求树的高度不能太高。实际上 B+ 树就是通过二叉搜索树推演改进的，我将在后面的文章再详细解释这个改进过程。

小结

哈希表适合等值查询，由于是无序的，区间查询会很慢。
有序数组适合等值和区间查询，但是数组具有连续性，插入和删除操作都可能需要移动其他元素。
二叉搜索树由于树的高度，区间查询需要中序遍历，都会导致查询效率很慢。
注意，在一些文章中经常会把 B+ 树说成 B 树或者 B-tree，这其实是错误的，B 树和 B+ 是两种不同的树，B+ 树是 B 树的一个优化，后面的文章我会再详细解释这个优化过程。
而且 B- 树其实也就是 B 树，这个符号并不是加减中的减号，并不是所谓的 “B 减树”，只是一个连接符号而已。
具体的原因
索引为什么要保存在硬盘中
首先要明白几个概念，服务器存储一般分内存和硬盘，内存的大小相对于硬盘来说是很小的。内存的访问速度是纳秒级别的，非常快，而硬盘的访问速度相对内存来说就比较慢了。
不管是访问内存还是硬盘数据，操作系统都是按数据页来读取数据的，即每访问一次硬盘或内存，只读取一页大小的数据，一页的大小约等于 4 kb，向硬盘读取数据的操作叫做磁盘 IO。
看到这里你或许会知道了 mysql 索引为啥不保存在内存中了吧，一方面是虽然内存访问速度快但容量一般都比较小，存不了多少数据，再一个 mysql 需要让数据持久化，如果服务器断电或异常重启会导致数据丢失。
怎么让二叉搜索树支持区间查询
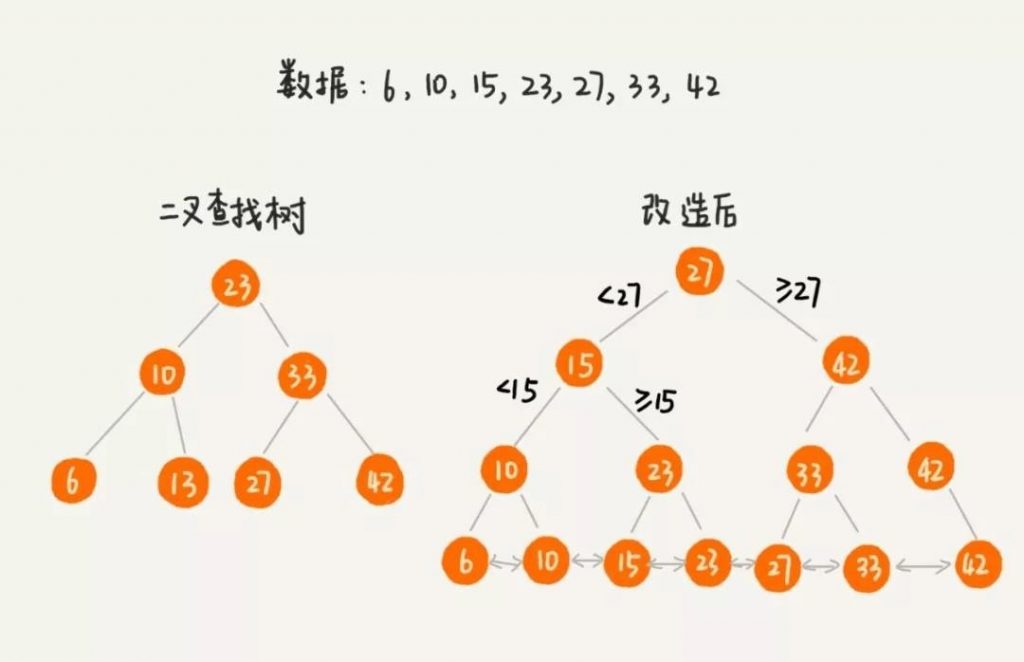
上面提到过二叉搜索树，为了让二叉搜索树也支持区间查询，我们把二叉树的叶子节点通过一个双向链表来连接，并且这个链表是有序的，注意叶子节点和普通节点是不一样的

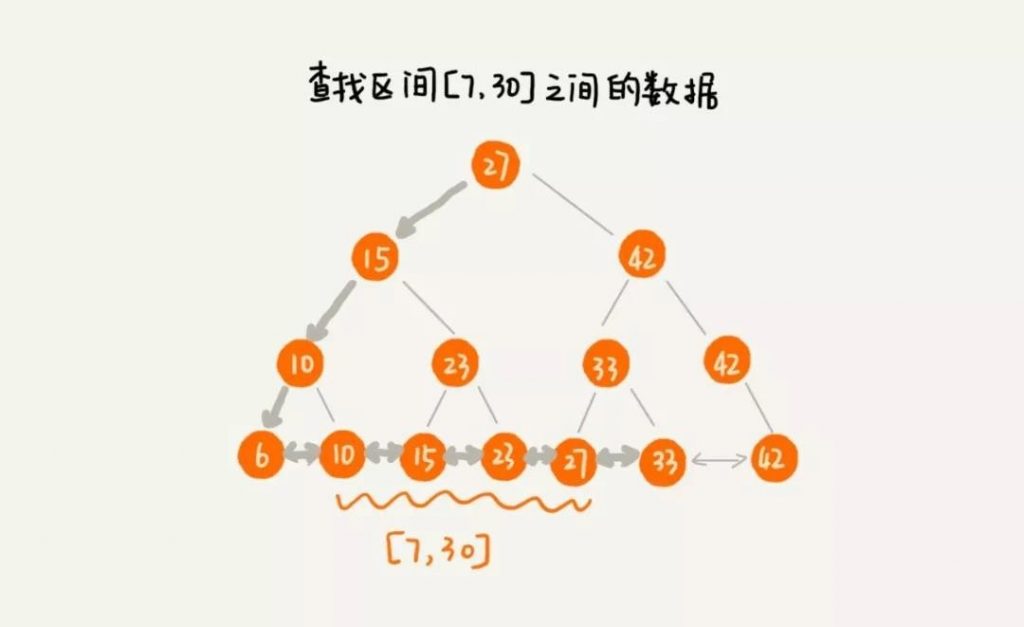
因此只需要先找到区间的起始值在链表中的位置，然后再往后遍历，直到遍历到区间的终止值，即可完成区间查询。如下图查找 7-30 这个区间的数据。

如何提升查询速度

因为二叉搜索树保存在硬盘中，我们每访问一个节点，就对应着一次硬盘 IO 操作，上面有说过向硬盘读取数据速度比较慢。因此树的高度就代表硬盘 IO 操作的次数，所以我们要想办法让树的高度变矮，来减少硬盘 IO。
要想树变矮一些，那就把树多分一些叉来吧，变成一颗多叉树。下面分别用二叉树和五叉树来存储 16 条数据，看下树的高度又怎样的变化。

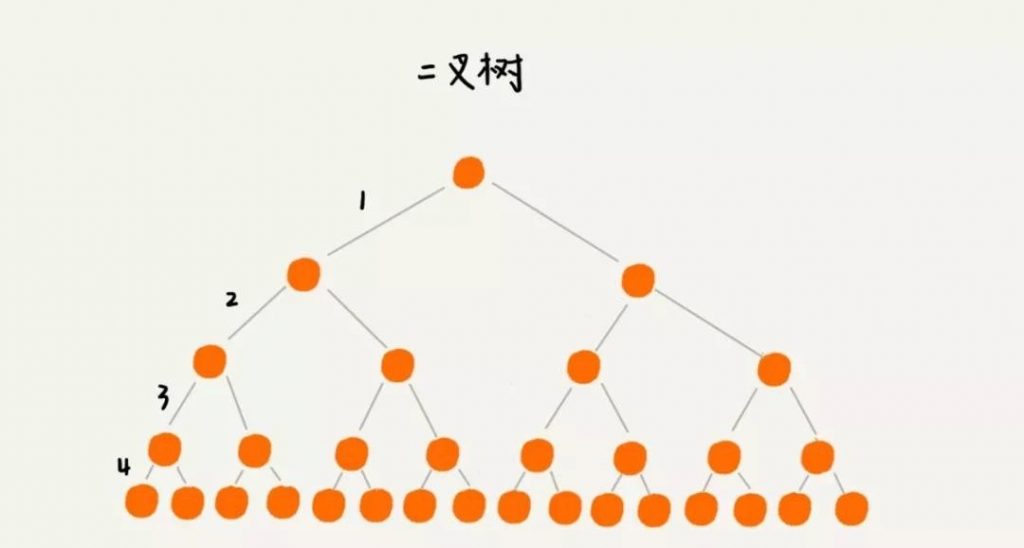
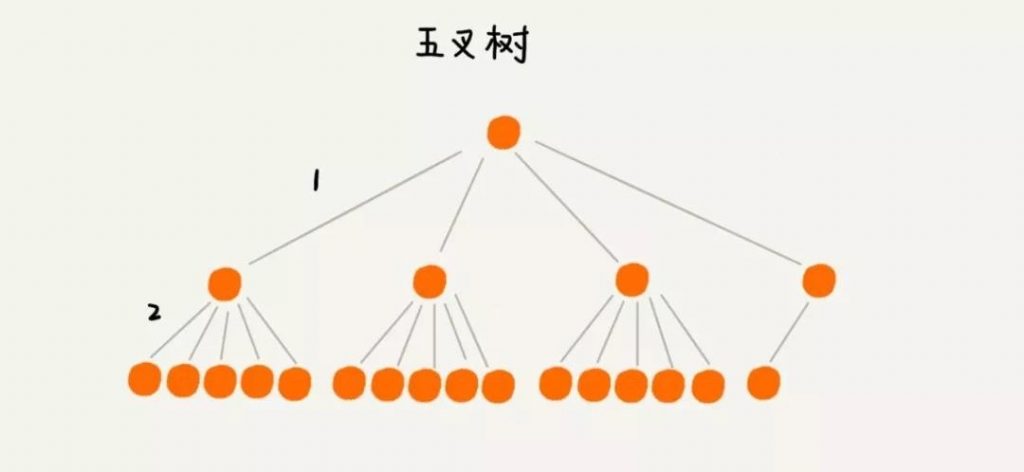
根节点一般存储在内存中，普通节点和叶子结点保存在硬盘中，因此显然二叉树的高度为 5，需要 5 次硬盘 IO，而五叉树的高度为 2，查询一个数据只需要 2 次硬盘 IO。
当然这仅仅是一个小数据的例子，如果有一亿条数据，我们构建一个 100 叉树，这棵树的高度也只有 3，因此多叉树能大大降低硬盘 IO，提升查询速度。
那么问题又来了，对于相同的数据量，是不是构建的多叉树的叉越多越好呢，因为叉越多树的高度就会越矮。

上面有说过操作系是按数据页大小来访问硬盘的，每次 IO 只读取一个数据页大小的数据，如果要读取的数据大于一个数据页，则会导致多次 IO。因此我们要尽量让每个节点的数据大小刚好等于一个数据页大小，即每访问一个节点只需一次 IO。

插入和删除数据怎么办

上面其实都是为了提高查询性能的，mysql 通常还有插入和删除操作的，这里我们再简单说一下 B+ 树如何处理插入和删除节点的操作。

这里我们把多叉树称作 m 叉树，这个 m 值是通过数据页大小和节点数计算出来的，尽量保证每访问一个节点就是一个数据页的大小，而且每个节点最多只有 m 个子节点。
现在我们要往数据库中插入新的数据，即要往 m 叉树中插入新的节点，这可能就会导致某些节点的子节点个数大于 m，也就会导致该节点大小大于一个数据页，访问该节点就需要多次 IO。
为了解决这个问题，m 叉树会把该节点分裂成两个节点，然后改分裂操作又会导致其父节点的子节点数可能超过 m，我们再用同样的方法分裂节点，一直影响到根节点。
删除操作也是类似的思想，如果有频繁的删除节点，就会导致某些节点的子节点过少，就会浪费存储空间并降低查询效率。所以就要想办法让这些节点合并起来，合并的话就有可能会导致其子节点数超过 m，超过的话就再用上面的分裂方法分裂子节点。
关于节点分裂和合并操作就简单说这些了，也不画图了，知道这个处理思想就好了。

下面再总结一下 B+ 树：
B+ 树就是一种多叉树，是由二叉搜索树不断演变过来的，为了满足区间快速查询，B+ 树的叶子节点通过双向链表串联起来。
这里使用双向链表是为了支持顺序和倒序查询，虽然双向链表相对于单向链表虽然会浪费一倍的指针空间，但是在硬盘中这点空间几乎微乎其微，用这点空间换时间是一件很值得的事情。
B+ 树的子节点数不超过 m 个，同时也不能少于 m/2 个，一旦超过就需要分裂，一旦少于就需要合并