多项式回归

理论上可以以上的方法拟合任何曲线，但前提条件是要事先对模型的形式进行判断，即知道非线性模型的参数设置。在一般情况下，通过绘制散点图的形式可以做到这一点。但是在更一般的情况下，如有多个自变量的情况下，无法绘制散点图，同时也很难对模型形式进行预估,这个时候可以使用本小节所介绍的方法。根据数学的相关理论，任何曲线均可以使用多项式进行逼近，这种逼近的分析过程即多项式回归。

多项式回归类似于可线性化的非线性模型，可通过变量代换的方式使用普通最小二乘对参数进行估计。

设有因变量y和自变量x，它们之间的关系为n次多项式的关系，则有如下模型：

令

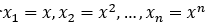
则多项式模型就转化为如下的多元线性模型：

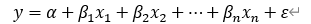
这样就可以按照多元线性回归模型进行分析了。对于多元的多项式模型：

同样做变量代换，令

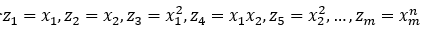
则有

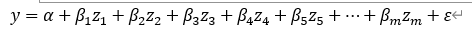
转化之后的模型同样可以按照多元线性回归模型进行分析。

多项式回归当阶数过高时，待估参数过多，在样本量不大的情况下会比较困难，这是多项式回归的一大缺陷。因此，一般的多项式回归模型很少应用到三阶以上。

一、Python代码实现多项式回归

1.模拟多项式回归的数据集

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)

# 一元二次方程
y = 0.5*x**2 + x + 2+np.random.normal(0,1,size=100)
plt.scatter(x,y)

2.使用线性回归拟合

很明显，用一根直线来拟合一根有弧度的曲线，效果是不好的

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X,y)
y_predict = lin_reg.predict(X) 
plt.scatter(x,y)
plt.plot(X,y_predict,color='r')

3.添加一个特征

X2 = np.hstack([X,X**2])
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)

# 由于x是乱的，所以应该进行排序
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

多项式回归线的绘制：

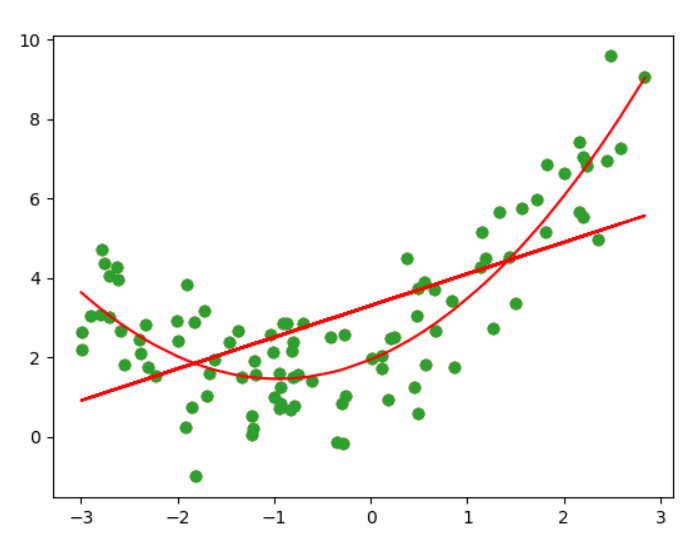
从上图可以看出，当添加了一个特征（原来特征的平方）之后，再从x的维度来看，就形成了一条曲线，显然这个曲线对原来数据集的拟合程度是更好的。

多线性回归在=算法上并没有新的地方，完全是使用线性回归的思路，关键在于为原来的样本，添加新的特征。而我们得到新的特征的方式是原有特征的多项式的组合。

采用这样的方式，我们就可以解决一些非线性的问题。

非线性回归