- Python数据分析教程导航
- Python - 操作 MySQL 数据库
- Python 数据分析教程
- Python 数据分析
- NumPy数值计算基础
- Python ndarray
- Python NumPy矩阵
- 利用NumPy进行统计分析
- Python pandas基础
- Python pandas数据结构
- Python pandas基本功能
- Python pandas描述性统计
- Python 数据读取、存储与⽂件格式
- 文本格式数据的读写
- Python 二进制格式
- 数据清洗与准备
- Python 处理缺失值
- Python 数据转换
- 字符串操作
- 分层索引
- 联合与合并数据集
- Python 数据重塑和数据透视
- Python Matplotlib数据可视化基础
- Python 常用绘图库原理及示例
- Python 用pandas和seaborn绘图
- Python 可视化工具概览
- Python Pandas的分组聚合操作
- GroupBy机制
- 数据聚合
- Python 数据透视表与交叉表
- 时间序列
- 日期和时间数据的类型及工具
- 时间序列基础
- 日期范围、频率和移位
- 时区处理
- 时间区间和区间算术
- 重新采样与频率转换
- 移动窗口函数
- Python pandas分类数据
- 分类数据
- Python GroupBy进阶
- Python 方法链技术
- Python建模库介绍
- Python pandas与建模代码的结合
- statsmodels介绍
- Python 使用sklearn转换器处理数据
- Python 构建并评价聚类模型
- Python 构建并评价分类模型
- 构建并评价回归模型
- Python ndarray对象内幕
- 高阶数组操作
- Python 广播
- Python 高阶ufunc用法
- Python 排序
- Python 回归分析
- 回归分析的基本原理
- 一元线性回归
- 非线性回归
- 多项式回归
Python 广播
广播
广播描述了算法如何在不同形状的数组之间进行运算。它是一个强大的功能,但可能会导致混淆,即使对于有经验的用户也是如此。最简单的广播示例发生在将标量值与数组组合的时候:

这里我们说标量值4已经被广播给乘法运算中的所有其他元素。
例如,我们可以通过减去列均值来降低数组中的每一列的数值。在这种情况下,它非常简单:
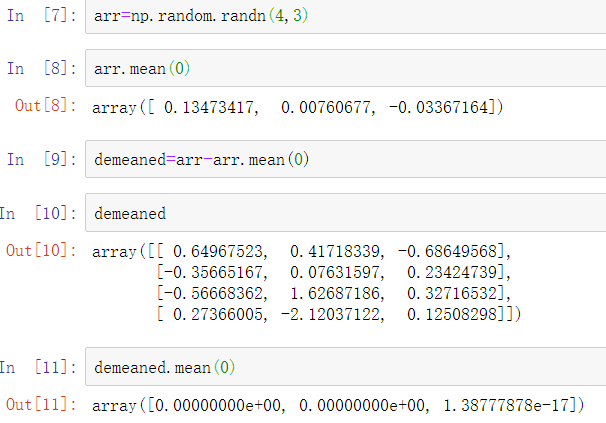
有关此操作的说明,请参见下图。对行进行减均值的广播需要更小心。幸运的是,只要遵循规则,就可以在数组的任何维度上对潜在较低维度值进行广播(例如从二维数组的每一列中减去行均值)。
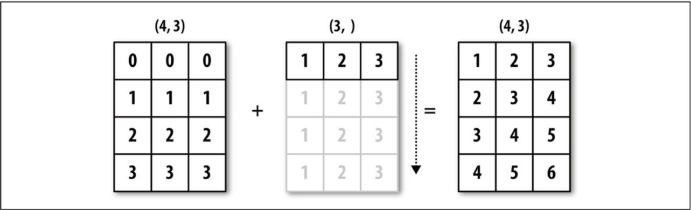
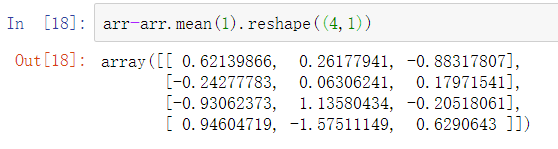
根据规则,为了从轴1减均值(即从每行减去行平均值),较小的数组的形状必须是(4, 1):
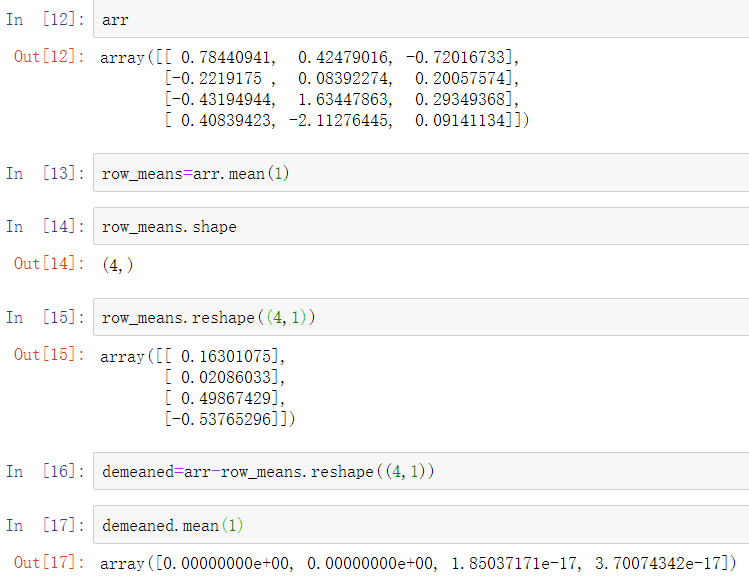
1、在其他轴上广播
使用更高维度的数组进行广播可能会更加令人头痛,但这确实是遵循规则的问题。如果不这样做,会得到这样的错误:
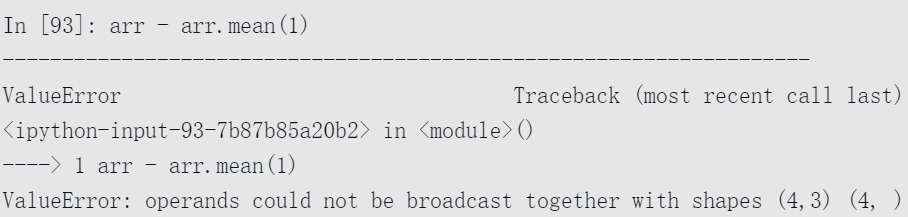
想要在轴0以外的轴上使用较低维数组进行算术运算是相当普遍的。根据广播规则,“广播维度”在较小的数组中必须为1。在这里显示的行减均值的例子中,这表示重新塑造行意味着形状是(4,1)而不是(4, ):
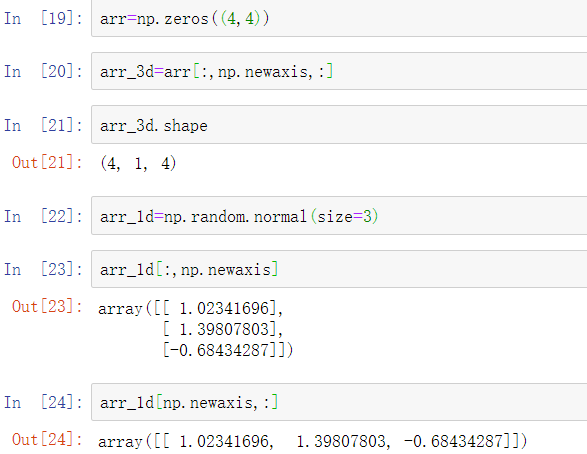
在三维情况下,在三个维度中的任何一个维度上进行广播只是将数据重塑为形状兼容的问题。
因此,一个常见的问题是需要添加一个长度为1的新轴,专门用于广播目的。使用reshape是一种选择,但插入一个轴需要构造一个表示新形状的元组。这通常是一个乏味的练习。因此,NumPy数组提供了一种通过索引插入新轴的特殊语法。使用特殊的np.newaxis属性和“完整”切片来插入新轴:
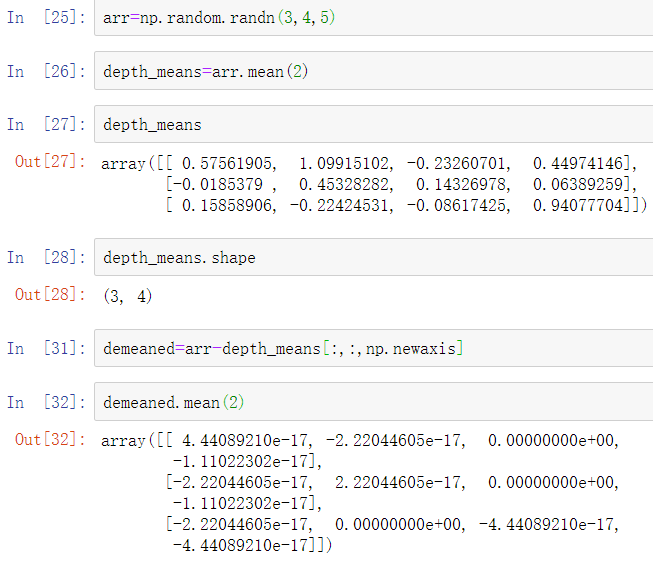
因此,如果有一个三维数组并想在轴2上减去均值,也就是说需要这样写:
2、通过广播设定数组的值
控制算术运算的相同广播规则也适用于通过数组索引设置值。在一个简单的例子中,我们可以做这样的事情:
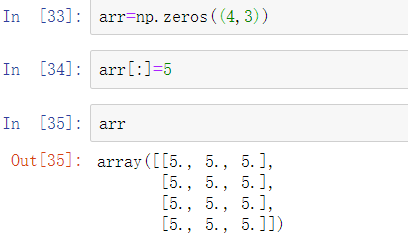
但是,如果想要将数值的一维数组设置到数组的列中,只要形状是兼容的就可以做到这一点:


